Materi Sistem Bilangan Real Lengkap dengan Penjelasannya

Sistem Bilangan Real
Sumber : educenter.id

Kalkulus - Pada artikel kali ini saya akan sedikit membahas tentang materi Sistem Bilangan Real, sebenartnya materi "Sistem Bilangan Real", sudah diajarkan dari SMP bahkan SD, namun untuk lebih tajam mengingat nya, maka diperlukan belajar berulang ulang.

Sistem matematika adalah himpunan unsur-unsur dengan operasi yang didefinisikan. Operasi-operasi yang telah kita kenal antara lain aljabar dan logaritma. Sedangkan sebagian himpunan dalam aljabar adalah himpunan-himpunan bilangan.

Apakah bilangan real itu dan apa sifat-sifatnya ? Untuk menjawabnya, kita mulai dengan beberapa sistem bilangan yang sederhana berikut ini.

1. Bilangan-bilangan bulat dan rasional

di antara sistem bilangan yang paling sederhana adalah bilangan-bilangan asli (= Natural), Contoh :
1, 2, 3, 4, 5, 6, 7, 8, 9, …
Dengan bilangan ini kita dapat menghitung: buku-buku kita, teman-teman kita, uang kita, dan lain sebagainya. Jika kita gandengkan negatifnya dan nol, kita akan peroleh bilangan-bilangan bulat (= dari bahasa Jerman, Zahlen):
…, -3, -2, -1, 0, 1, 2, 3, …

Bila kita mencoba mengukur panjang, berat benda, atau tegangan listrik, bilangan-bilangan bulat tidak akan memadai. Bilangan ini terlalu kurang untuk memeberikan ketelitian yang cukup dalam sebuah pengukuran. Kita dituntut untuk juga mempertimbangkan hasil bagi (rasio) dari bilangan-bilangan bulat, yaitu bilangan-bilangan seperti:

Bilangan-bilangan yang dapat dituliskan dalam bentuk , dimana m dan n adalah bilangan bulat dan , disebut bilangan-bilangan rasional (= Quotient ).

Apakah bilangan rasional berfungsi mengukur semua panjang? Fakta yang mengejutkan ini ditemukan pertama kali oleh orang Yunani kuno beberapa abad sebelum masehi. Mereka memperlihatkan bahwa meskipun merupakan panjang sisi miring sebuah segi tiga siku-siku dengan sisi 1 , bilangan ini tidak dapat dituliskan sebagai suatu hasil bagi dua bilangan bulat. Jadi adalah suatu bilangan tak rasional (irasional).

Demikian juga Jika kita belum terbiasa untuk bisa membedakan bilangan rasional dan bilangan irasional secara langsung, maka ada satu ciri khusus yang yang bisa kita jadikan pedoman untuk membedakan keduanya.

2. Bilangan-bilangan real

Sekumpulan bilangan (rasional dan irasional) yang dapat mengukur panjang, bersama-sama dengan negatifnya dan nol kita namakan bilangan-bilangan real. Atau dengan kata lain, bilangan real adalah bilangan yang dapat berkoresponden satu-satu dengan sebuah titik pada garis bilangan. Pada garis bilangan tersebut terdapat titik asal yang diberi lambang 0 (nol) sebagai titik awal untuk mengukur jarak ke arah kanan atau kiri. Setiap titik pada garis bilangan mempunyai lambang yang tunggal, disebut koordinat titik, dan garis bilangan yang dihasilkan diacu sebagai garis real.

Dengan mengetahui anggota dari masing-masing himpunan bilangan yang termasuk kelompok bilangan real, bagaimanakah hubungan masing-masing himpunan bilangan asli, bilangan cacah, bilangan bulat, bilangan rasional, bilangan real, dan bilangan kompleks jika kita gambarkan dalam diagram venn?

3. Operasi pada Bilangan Real

Operasi penjumlahan, pengurangan, perkalian, dan pembagian.

a) Operasi penjumlahan

Contoh:
1. 4 + 6 = 10
2. 4 + (-6 ) = -2

b) Operasi pengurangan

Contoh:
1. -6 – 5 = -6 + (-5) = -11
2. 3 -6 – 4 = -6 + (-4) = -10

c) Operasi perkalian

Contoh:
1. 6 x 5 = 30
2. 6 x (-4) = -24
3. (-6) x (-4) = 24

d) Operasi pembagian

Contoh:
1. 12 : 2 = 6
2. 12 : -2 = -6
3. (-12) : (-2) = 6

4. Menghitung persentase

a) Komisi

Komisi adalah pendapatan yang besarnya tergantung pada tingkat penjualan yang dilakukan
Contoh:
Seorang salesman akan mendapatkan komisi sebesar 15 % jika ia mampu menjual barang senilai Rp. 2.000.000,00. tentukan besarnya komisi yang diterima?
Jawab:
Komisi = 15 % x Rp. 2.000.000
Jadi besarnya komisi yang diterima oleh salesman itu sebesar. Rp. 300.000,00

b) Diskon

Diskon adalah potongan harga yang diberikan
Contoh:

Menjelang miladnya, sebuah toko serba ada memberikan diskon sebesar 25% untuk semua produk. Jika kita berbelanja senilai Rp. 800.000,00, berapa kita harus membayar?
Jawab:

Diskon = 25 % x Rp. 800.000,00
Jadi, kita harus membayar sebesar:
Rp. 800.000,00 – Rp. 200.000,00 = Rp. 600.000,00

c) Laba dan rugi

Laba diperoleh jika harga penjualan lebih dari harga atau biaya pembelian. Rumusnya sebagai berikut LABA = PENJUALAN – PEMBELIAN. Rugi diderita jika harga penjualan kurang dari harga atau biaya pembelian. Rumusannya sebagai berikut
RUGI = PEMBELIAN - PENJUALAN
Contoh:

Sebuah barang dibeli dengan harga Rp. 2.000.000,00, dan di jual dengan harga Rp. 2.400.000,00. Hitunglah persentase keuntungan dari harga pembelian dan dari harga penjualan!
Jawab:
Laba = Rp. 2.400.000,00 – Rp. 2.000.000,00 = Rp. 400.000,00

d) Persentase keuntungan (laba) dari harga beli

Persentase keuntungan (laba) dari harga penjualan:
P%= Rp.400.000 x 100%=16.7%
Rp.2400.000

5. Macam-macam Bilangan Real

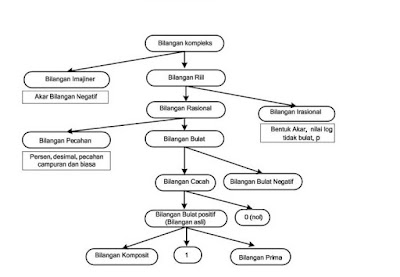Macam Macam Bilangan Real

A. Bilangan Asli (A)

Bilangan asli adalah suatu bilangan yang mula-mula dipakai untuk
membilang. Bilangan asli dimulai dari 1,2,3,4,…
A = {1,2,3,4,…}

B. Bilangan Genap (G)

Bilangan genap dirumuskan dengan 2n, nÎA
G = {2,4,6,8,…}

C. Bilangan Ganjil (Gj)

Bilangan ganjil dirumuskan dengan 2n -1, nÎA
Gj = {1,3,5,7,…}

D. Bilangan Prima (P)

Bilangan prima adalah suatu bilanganyang dimulai dari 2 dan
hanya dapat dibagi oleh bilngan itu sendiri dan ± 1
P = {2,3,5,7,…}

E. Bilangan Komposit (Km)

Bilangan komposit adalah suatu bilangan yang dapat dibagi oleh bilangan yang lain
Km = {4,6,8,9,…}

F. Bilangan Cacah (C)

Bilangan Cacah adalah suatu bilangan yang dimulai dari nol
C = {0,1,2,3,4,…}

G. Bilangan Bulat (B)

Bilangan bulat terdiri dari bilangan bulat negatif, bilangan nol, dan bilangan bulat positif.
B = {…,-4,-3,-2,-1,0,1,2,3,4,…}

H. Bilangan Pecahan (Pc)

Bilangan pecahan adalah suatu bilangan yang dapat dinyatakan
dalam bentuk a/b, a sebagai pembilang dan b sebagai penyebut,
dengan a dan b ÎB serta b ≠0

I. Bilangan Rasional (Q)

Bilangan rasional adalah suatu bilangan yang dapat dinyatakan
dalam bentuk , a dan b ÎB serta b ≠0. (Gabungan bilangan bulat
dengan himpunan bilangan pecahan)

J. Bilangan Irasional (I)

Bilangan irasional adalah suatu bilangan yang tidak dapat
dinyatakan dalam bentuk , a dan b ÎB serta b ≠0.
Contoh: π = 3,14159…, e = 2,71828….

K. Bilangan Real (R)

Bilangan real adalah suatu bilangan yang terdiri dari bilangan
rasional dan bilangan irasional. Bilangan real biasanya disajikan
dengan sebuah garis bilangan.
Contoh:

-1 -2 -3 0 1 2 3 4

L. Bilangan Khayal (Kh)

Bilangan khayal adalah suatu bilangan yang hanya bisa dikhayalkan dalam pikiran, tetapi kenyataannya tidak ada.

M. Bilangan Kompleks (K)

Bilangan Kompleks adalah suatu bilangan yang terdiri dari bilangan dan khayal.

6. Sifat-sifat Operasi Bilangan Bulat

a. Sifat Komutatif

a + b = b + a
a.b = b.a

Contoh:
1. 5 + 6 = 6 + 5 = 11
2. 9 . 3 = 3 . 9 = 27

b. Sifat Assosiatif

(a + b) + c = a + (b + c)
(a . b) . c = a . (b . c)

Contoh:
1. (5 + 2) + 3 = 5 + (2 + 3) = 10
2. (5 x 2) x 3 = 5 x (2 x 3) = 30

c. Sifat Distributif Perkalian Terhadap Penjumlahan

a x (b + c) = ab + ac

Contoh:
5 x (3 + 6) = 5 . 3 + 5 . 6= 15 + 30= 45

d. Terdapat Dua Elemen Identitas

Setiap bilangan a mempunyai dua elemen identitas, yaitu 1 dan 0,sehingga memenuhi:
a + 0 = a
a . 1 = a

e. Terdapat Elemen Invers

Setiap bilangan a mempunyai balikan atau invers penjumlahan, yaitu –a yang memenuhi:
a + (-a) = 0
Setiap a ≠ 0 mempunyai balikan perkalian.

Demikianlah Artikel tentang Materi Sistem Bilangan Real Lengkap dengan Penjelasannya
Semoga Bermanfaat dan Tetap Pantengin Website ini yahhh